- 直流って何?
- 交流って何?
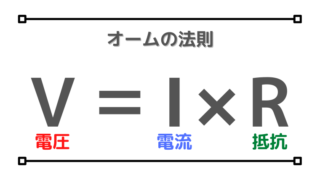
- オームの法則は直流・交流どちらも使えるの?
今回の記事はこのような疑問を解決するために書きました。
こんにちは!クマペイです!
当たり前のように感じていることを説明するのって意外に難しいですよね。
そんなことの一つが「直流と交流の違い」です。
そして電気の基礎であるオームの法則は直流でも交流でも使うことができるのか?
結論としては、使えるけどコイルやコンデンサがあるときは注意が必要。
(オームの法則の簡単な解説はこちら)
ですのでこの記事ではこのようなことを簡単に解説していきます。
- 直流とは
- 交流とは
- 直流と交流のオームの法則
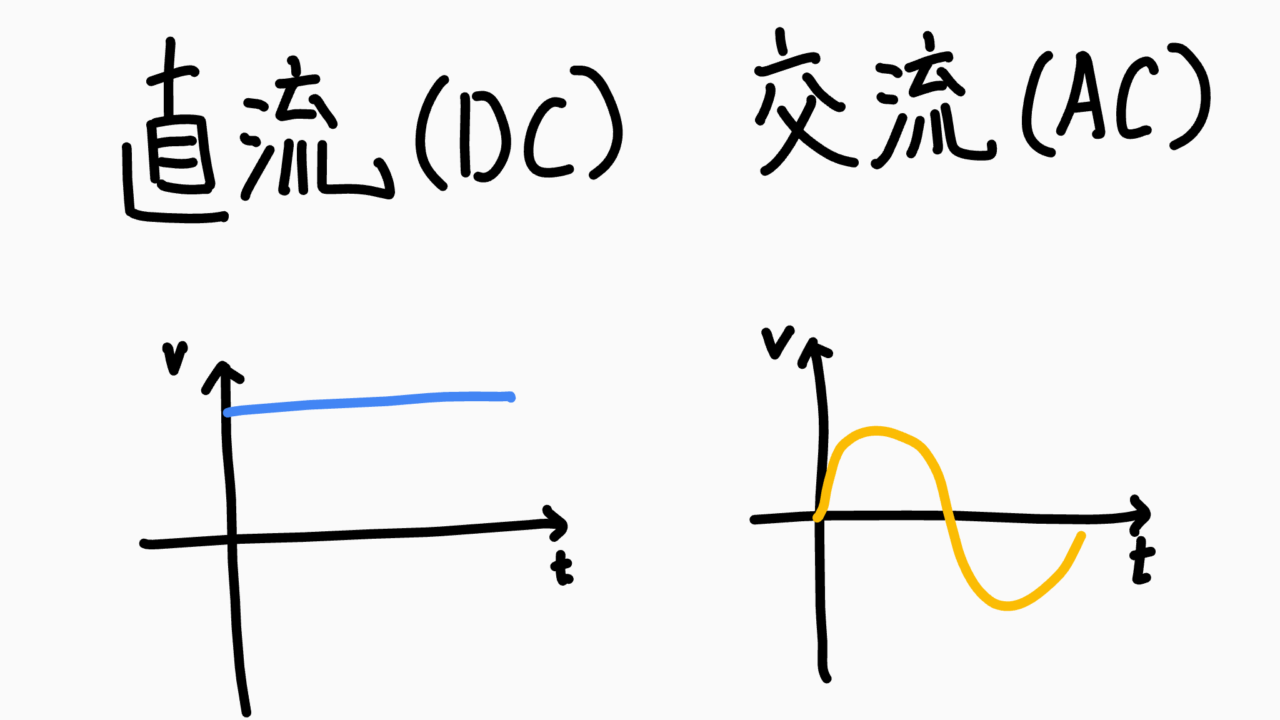
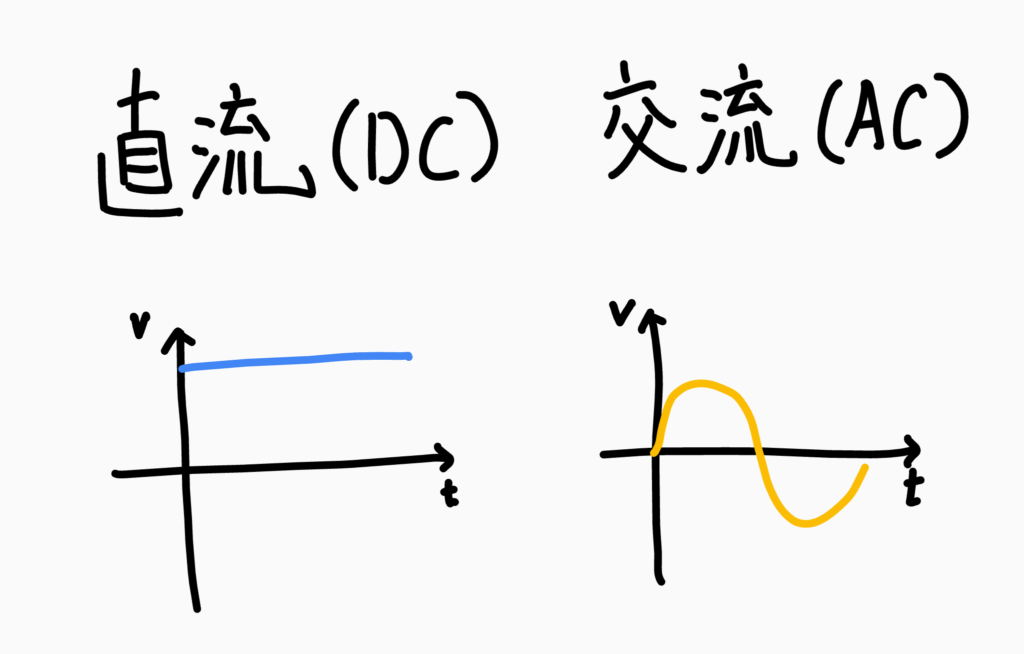
直流(Direct Current)とは
電流の向きが一定でその大きさが変化しないもの
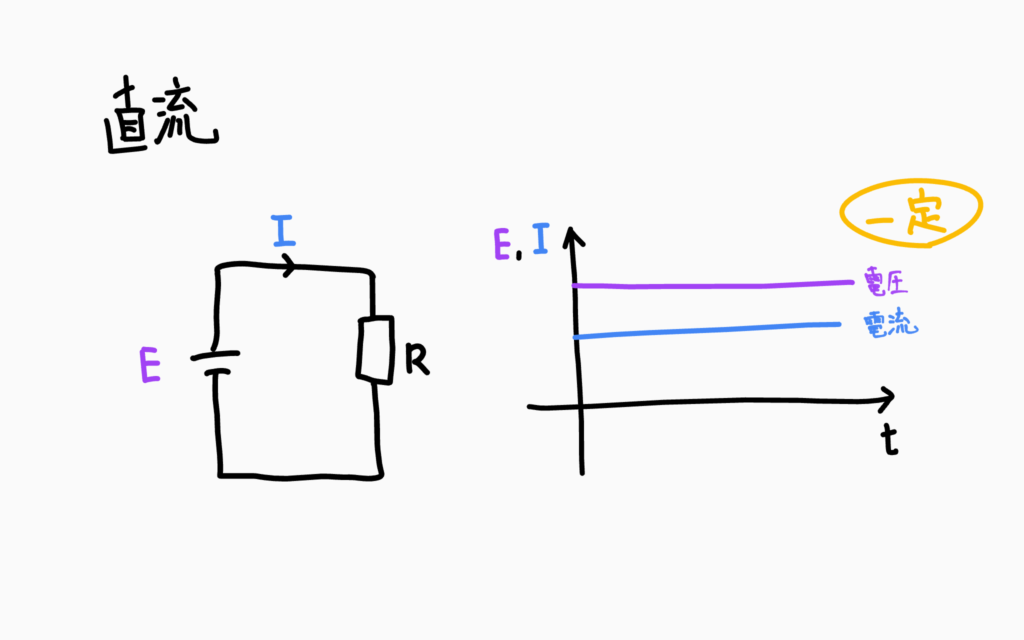
それぞれのアルファベットの意味はこちらになっています。
- E:電源電圧
- I:電流
- R:抵抗
- t:時間
グラフから、時間(t)が進んでも電圧(E)と電流(I)はプラスの方向へ流れていることがわかります。
交流(Alternating Current)とは
電流の向きと大きさが周期的に変化するもの
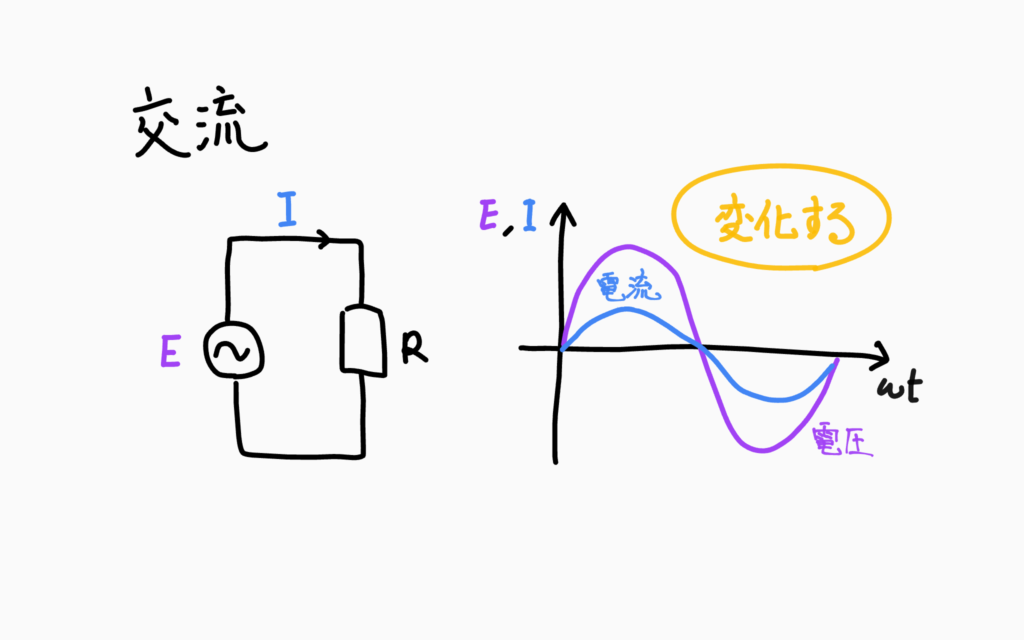
それぞれのアルファベットの意味はこちらになっています。
- E:電源電圧
- I:電流
- R:抵抗
- ω:角速度
- t:時間
交流は周期的に電流・電圧が変化するので角速度という要素が出てきます。
ただ今回はオームの法則が使えるかどうかなので、この辺については割愛して問題ありません。
グラフから、電圧と電流が周期的に変化していることがわかればOKです!
直流と交流のオームの法則
では直流と交流でオームの法則を使ってみましょう。
条件を揃えるために同じ電気回路の電源を直流か交流にしたもので計算してみます。
今回使用する回路はこちら
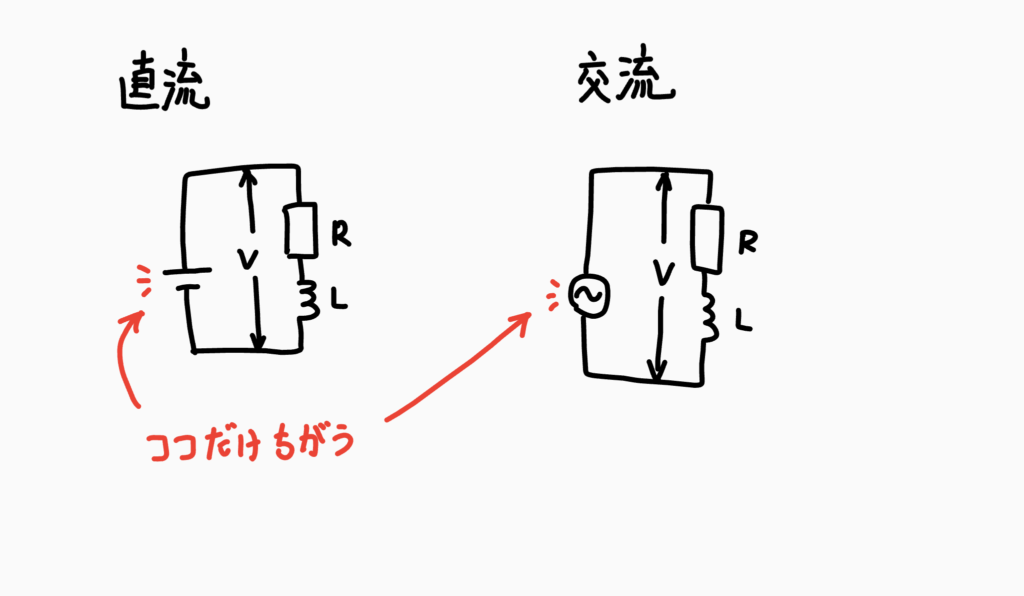
直流のオームの法則
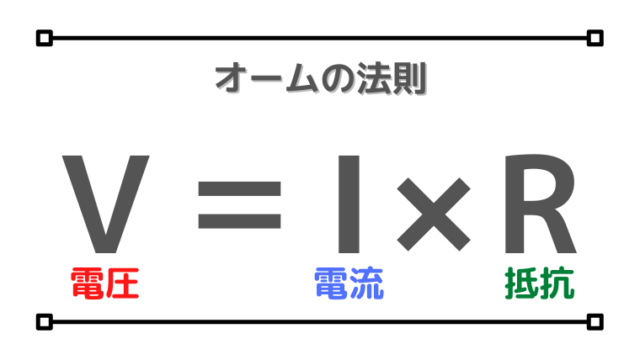
$${V}={R}\times{I}$$
いつものオームの法則ですね。
直流の場合、コイルのことは無視して構いません。(コンデンサのことは無視できません)
理由としては、過渡現象によって一定時間後に電流の流れが定常状態になるためです。
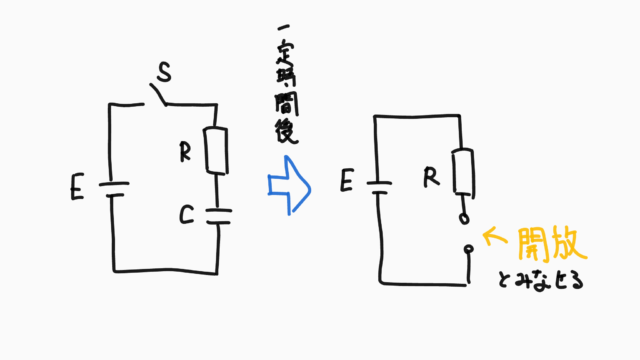
過渡現象
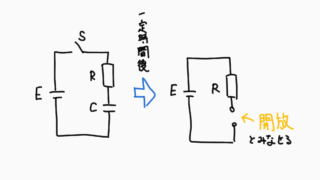
過渡現象とは、回路にコンデンサやコイルがあるときに、スイッチを閉じたり開いたりした瞬間に電流や電圧が時間的に変化する現象のことです。
例えばコイルが入った回路とグラフを図に示すとこんな感じになります。
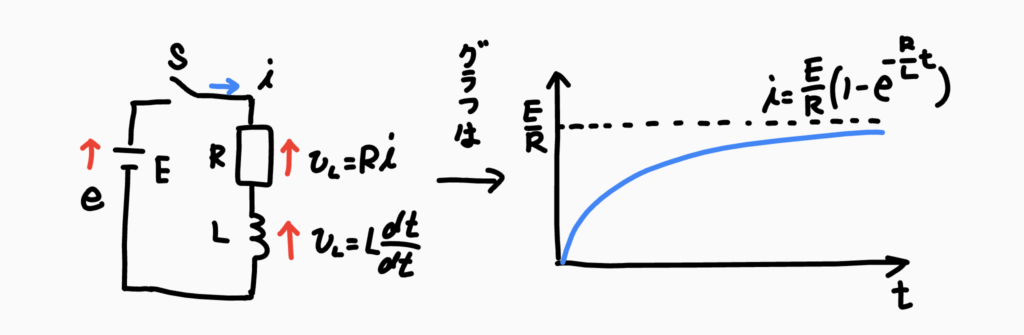
ちょっと何言ってるかわかんないですね。
今回は「そんなこともあるんだ〜」程度で大丈夫です。
交流のオームの法則
$$\dot{V}=\dot{Z}\times\dot{I}$$
こちらの式で計算が可能ですが、\(\dot{Z}\)という文字が出てきました。
\(\dot{Z}\)はインピーダンスというものです。
交流でオームの法則を使うにはインピーダンスを知っておく必要があります。
電流の流れにくさを表したもので、直流電源回路で言う抵抗のことです。
- 抵抗
- インダクタンス
- 静電容量
インピーダンスは上記の3つで構成されます。単位はオームです。
今回の回路では抵抗とコイルがあるので\(\dot{Z}\)は下記のようになります。
$$\dot{Z}={R}+{jωL}$$
抵抗Rだけのときは直流と同じように計算すれば良いのですが、コイルやコンデンサが回路に入っている場合、このような形になってしまうことを知っておきましょう。
最後に
直流…電流の向きが一定でその大きさが変化しないもの
交流…電流の向きと大きさが周期的に変化するもの
オームの法則は直流・交流どちらにも使用できる
ただしコイルやコンデンサがあるときは注意が必要
ということで、直流・交流とオームの法則についてサラッと解説しました。
それぞれの詳しい解説は他の記事で行います!
以上!